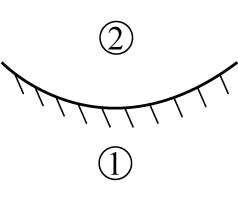The objective of this study is to reveal a non-trivial effect of the interfacial curvature on stability of uniformly and suddenly (in time) accelerated interfaces, such as liquid rims. The systematic approach developed in the course of this work also provides a rigorous generalization of the widely accepted ad hoc idea, due to Layzer [Astrophys. J. 122, 1-12 (1955)], of approximating the potential velocity field near the interface.

This is a collaborative effort with Jerrold E. Marsden (Caltech) on a systematic development of a rigorous nonlinear stability theory for infinite-dimensional dissipative and conservative systems (Navier-Stokes and other field equations), which, in particular, aims to understand the interrelation between transient growth and nonlinear effects in the problem of transition.

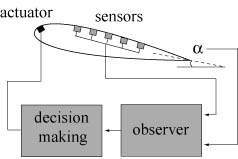In this joint work with Jerrold E. Marsden (Caltech) and Hassan M. Nagib (IIT) we uncover the low-dimensional nature of the complex dynamics of actuated separated flows. Namely, motivated by the problem of model-based predictive control of separated flows, we identify the requirements on a model-based observer and the key variables and propose a prototype model in the case of thick airfoils as motivated by practical applications.

The goal of this work is to develop a coherent theory of the counter-intuitive phenomena of dynamical destabilization of finite- and infinite-dimensional systems under the action of dissipation. We have put the main theoretical achievements in a general context, thus unifying the current knowledge in this area and the multitude of relevant physical problems scattered over a vast literature. This general view also highlights the striking connection to various areas of mathematics.

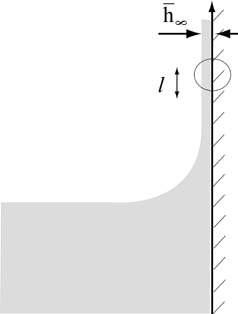In this work we studied deviations from the classical Landau-Levich law in the problem of dip coating caused by the nature of the liquid-gas and liquid-solid interfaces. Our theory based on a purely hydrodynamic role of the surface active substance suggests that there is a sorption-controlled coating regime in which Marangoni effects should lead to film thinning. However, our experiments conducted in this regime demonstrate film thickening, calling into question the conventional wisdom, which is that Marangoni stresses lead to film thickening. Next we examine the effect of well-characterized substrate roughness on the coated film thickness. In particular, it is found that roughness results in a significant thickening of the film relative to that on a smooth substrate and a different power of capillary number than the classical Landau-Levich law.

According to the Saffman-Taylor criterion there is no instability when a more viscous fluid is displacing a less viscous one in a Hele-Shaw cell. Yet an instability was observed experimentally in the same classical set-up but with the inner walls of the cell coated with surfactant solution. Linear stability analysis revealed the basic mechanism of this new instability in agreement with our experiments. Our experimental study also quantified the nonlinear evolution of fingering and its various steady and unsteady patterns.

The general classical Lighthill problem of propagation of two- and three-dimensional disturbances in viscous super- and hyper-sonic flows is solved exactly in the framework of characteristic analysis. Unlike previous results for linear disturbances we deduce a condition determining nonlinear characteristic surfaces which is exact and therefore allows both qualitative and quantitative studies of the speed of propagation as a function of various physical phenomena. These include negative and adverse pressure gradients, and effects of wall cooling and suction-blowing.

The problem of self-similar solutions for steady wall jets is considered in the context of two- and three-dimensional Prandtl boundary layer equations, and three-dimensional parabolized Navier-Stokes equations for Newtonian and non-Newtonian fluids. In contrast to dimensional analysis, which does not allow one to determine self-similar solutions in this case, a generating functions approach enabled us to derive conservation laws for the aforementioned problems and, as a consequence, to find new self-similarities of the Navier-Stokes equations.