definition of a Laplace transform
Welcome to Vibration Data
|
Laplace transforms are used to solve differential equations. As an example, Laplace transforms are used to determine the response of a harmonic oscillator to an input signal. |
|
|
|
|
|
| 1.1 |
|
definition of a Laplace transform |
| 1.2 |
|
|
| 1.3 |
|
|
| 1.4 |
|
|
| 1.5 |
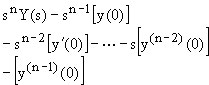 |
|
| 1.6 |
|
|
| 1.7 |
|
|
| 1.8 |
|
|
| 1.9 |
|
|
| 1.10 |
|
|
| 1.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(t) |
|
|
 |
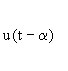 |
|
|
|
|
|
|
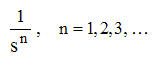 |
|
|
|
|
|
|
|
|
the Gamma function is given in Appendix A |
|
|
|
|
|
|
|
|
| 2.11 |
|
 |
| 2.12 |
|
|
| 2.13 |
|
|
| 2.14 |
|
|
| 2.15 |
 |
|
| 2.16a |
|
|
| 2.16b |
|
|
| 2.17 |
|
|
| 2.18 |
 |
|
| 2.19 |
|
|
| 2.20 |
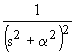 |
|
| 2.21 |
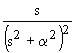 |
|
| 2.22 |
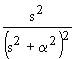 |
|
| 2.23 |
|
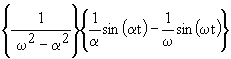 |
| 2.24 |
|
|
| 2.25 |
|
|
| 2.26 |
|
|
| 2.27 |
|
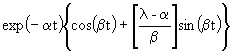 |
| 2.28 |
|
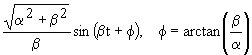 |
| 2.29 |
|
|
| 2.30 |
|
|
| 2.31 |
|
|
| 2.32 |
|
|
| 2.33 |
|
|
| 2.34 |
|
|
| 2.35 |
|
Bessel function given in Appendix A |
| 2.36 |
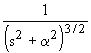 |
|
| 2.37 |
|
Modified Bessel function given in Appendix A |
| 2.38 |
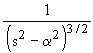 |
|
| 2.39 |
|
 |
Examples of the Laplace Transform as a
Solution for Mechanical Shock and Vibration Problems:
|
References1.
Jan Tuma, Engineering Mathematics Handbook, McGraw-Hill, New
York, 1979.
|
|
Please send comments and questions to
Tom Irvine at: tomirvine@aol.com
|